从钢化玻璃诞生开始,就伴随着自爆问题。钢化玻璃自爆可以表述为钢化玻璃在无外部直接作用的情况下而自动发生破碎的现象。在钢化加工、贮存、运输、安装、使用等过程中均可发生钢化玻璃自爆。自爆按起因不同可分为两种: 一是由玻璃中可见缺陷引起的自爆,例如结石、砂粒、气泡、夹杂物、缺口、划伤、爆边等; 二是由玻璃中硫化镍(NIS)杂质和异质相颗粒引起钢化玻璃自爆。这是两种不同类型的自爆,应明确分类,区别对待,采用不同方法来应对和处理。前者一般目视可见,检测相对容易,故生产中可控。后者则主要由玻璃中微小的硫化镍颗粒体积膨胀引发,无法目测检验,故不可控。而上海美特幕墙有限公司的萧愉、朱齐飞、卢少龙等专家,通过多年来丰富的临场经验和案例汇总分析,推出“幕墙玻璃破损概率的估算探讨”一文,希望能够为广大幕墙、门窗的工程施工单位,以及玻璃深加工企业、材料厂商,带来更多的启迪与指导!
摘要:对实测数据经统计分析,用正交表判别影响强度分布因子的显著相关因素,采用回归经验公式计算玻璃破损率,以此为基础计算玻璃面板许可应力和跨中挠度,较为符合实际。
关键词:幕墙玻璃面板;强度分布因子;玻璃破损率;许可应力;跨中挠度;回归经验公式;脆性材料微裂缝扩展。
一、试验实测数据分析
1. 上海交银金融大厦1999年9月20日由上海建科检测。玻璃面板为8mm钢化+12A+6mm浮法贴膜中空玻璃,等效厚度te=8.55mm,面积A=a×b=1471×2950mm=4.34㎡。跨中挠度实测数据及与规范JGJ102公式计算、几何非线性有限元方法计算结果对比,见表一。发现:
1) 规范JGJ102公式计算结果和实测值比较,误差很大为57.34~82.15%,平均为66.61%;
2) 几何非线性方法计算结果值比规范公式计算值小,但和实测值比较,误差仍大为49.18~22.88%,平均为31.49%。
2. 上海久事大厦1998年8月26日,上海美特幕墙有限公司采用“水压法”检测并由上海建科检测中心监察。玻璃面板为10mm钢化+12A+8mm浮法中空玻璃,等效厚度te=10.90mm,面积A=a×b=1572×3965=6.233㎡。跨中挠度实测数据及水压W水与挠度df二元一次回归方程(相关系数r=0.9929)计算数据见表四。发现回归方程计算值与实例值误差较小,平均为3.38%。
二、对幕墙玻璃面板应力、挠度计算问题的疑惑与矛盾
1. 玻璃是没有预兆的突然脆性断裂的脆性材料,不是弹性材料,应力应变关系呈直线,但采用弹性力学方法计算,虽然是在直线阶段取值,不同玻璃的应力-应变线并不完全相同。
2. 所有的玻璃都是由于表面裂纹扩展而破碎,应采用材料断裂力学表面裂纹理论来分析。在美国标准ASTM E1300有玻璃破损概率近似估算公式,包含了由表面微裂纹确定的参数。
3. 玻璃的实际强度取决于其表面随机微观和宏观裂纹的存在及其损伤程度与完备性。因此,玻璃破坏强度有非常大的离散性。应用统计方法表征玻璃力学性能的这一特征,规定其离散度、许可临界值、保证率等。不同玻璃强度的正态分布都不相同。玻璃的破坏是由强度控制的。
4. 玻璃生产的原材料、配方、工艺参数、管理控制水平都有较大差异。玻璃产品的强度设计值等,应由供应玻璃的生产厂家提供的个性批量测试数据作为设计的依据,而不是采用普遍适用的一般性的常数值。各不同玻璃产品,性能指标有不同,强度更不一。
5. 规范中规定的最大应力σ、跨中挠度df的计算公式是在弹性小挠度情况下推导出来的,况且不论材料的不同,如玻璃面板、石材面板、金属面板等,都取同一计算公式,其计算结果不能反映实际受力和变形状态,偏大较多约30%-50%。此弹性小挠度计算公式再加大挠度方程折减系数的结果已超出了“挠度不大于玻璃板厚度的适用范围” 。
6. 关于玻璃面板的最大许用面积,几本规范标准的规定数据不一致。所规定的限值依据是什么?为什么?没有解释、缺少分析,究竟如何确定相互有矛盾。
7. 玻璃的实际强度取决于其表面损伤程度的变量,微裂纹的尺寸和分布是关键因素,面积增大、荷载持续时间延长都使临界裂纹形成概率提高即玻璃面板的破坏概率增大。而多数玻璃力学参数都是小尺寸试件,短时间荷载试验的结果,误差会很大。
有鉴于此,作者认为以大量实测实量的测试数据为基础,经过统计分析,采用由试验数据归纳得出的经验回归公式较为符合实际,也使用方便、简约。
三、计算思路

其中WK:为风荷载标准值(KPa)
A:为玻璃面板面积(㎡)
t:为玻璃面板厚度(mm)
E:为玻璃材料弹性模量(N/m㎡)

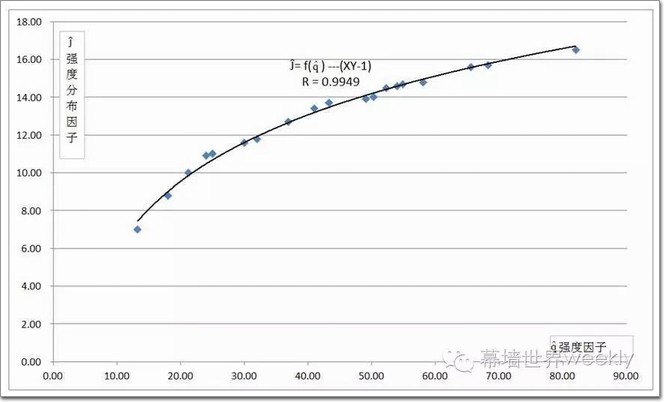

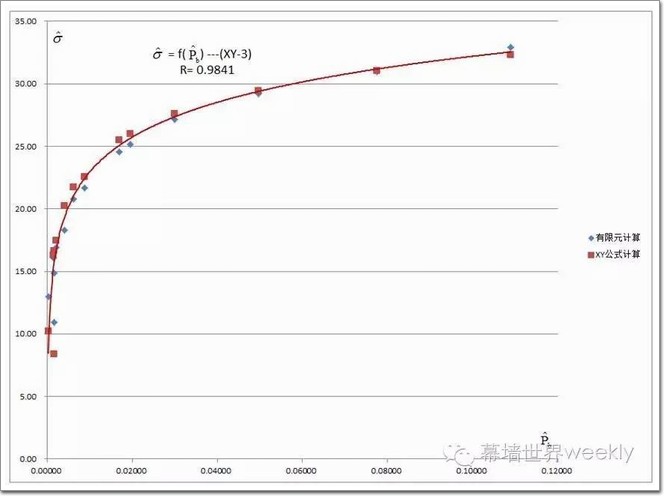

四、计算实例


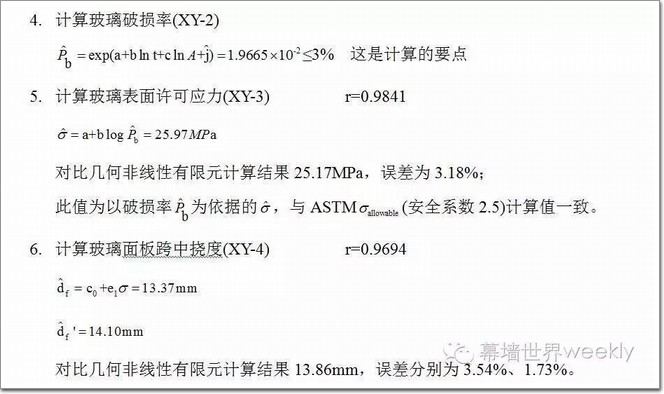
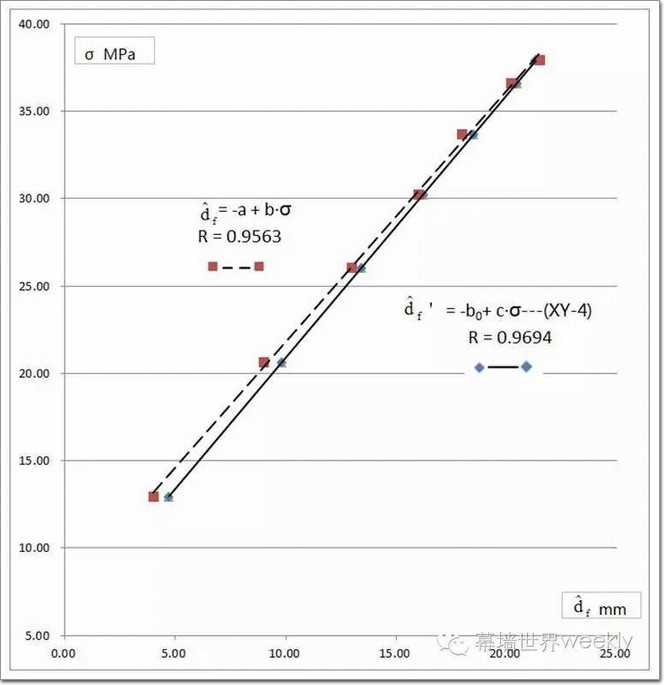
五、电算制表

六、计算验证
作者归纳的回归经验公式(XY-1、2、3、4)由于国内尚未见到有关玻璃板片微裂缝扩展断裂力学试验数据,故拿来美国标准ASTM E1300估算玻璃无量纲强度因子、强度分布因子、玻璃破损率和表面许可最大应力的回归经验公式,这些公式都是建立在大量试验测试数据的基础上的。同时作者又根据几何非线性有限元方法计算的结果加以对比结合。为了证实计算结果的可用性,作者对中国行业标准JGJ113所列条文说明的玻璃板片测试结果和上海建科检测中心对上海交银金融大厦、久事大厦玻璃面板的检测结果进行了对照,发现两者之间符合较好,误差较小。
作者这一计算有实际的试验测试数据为基础,经统计分析,建立在脆性材料玻璃微裂缝扩展理论导出的经验回归方程,结合了几何非线性有限元计算结果和ASTM经验公式。从对试验数据的符合性看,介于规范公式计算值和几何非线性有限元计算值之间相一致的。计算程序简单、快捷、实用。
1. 交银金融大厦
1999年9月20日上海建科检测,玻璃面板8mm钢化+12A+6mm浮法贴膜中空玻璃,面积A=a×b=1471×2950mm=4.34㎡,等效厚度te=8.55mm。
2. 久事大厦
1998年8月26日,上海美特幕墙有限公司水压法检测并由上海建科监察,玻璃面板10mm钢化+12A+8mm浮法中空玻璃,面积A=a×b=1572×3965mm=6.233㎡,等效厚度te=10.9mm。



3. JGJ113-2003条文说明P.58玻璃抗风压设计数据和作者提出的XY公式计算数据对比:面积:A=axb=1500×1800mm=2.7㎡,厚度t=8mm,普通浮法玻璃大批量风压破坏试验数据表:
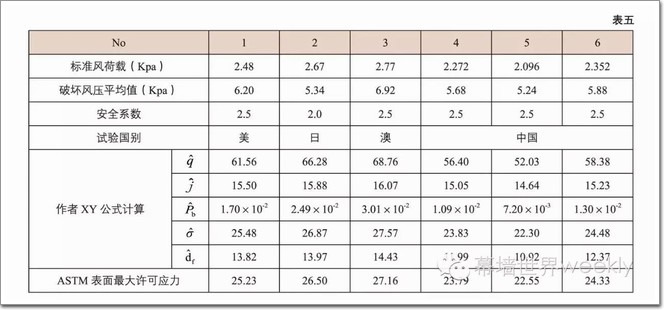

4. 26组规范公式计算、几何非线性有限元计算和作者归纳XY程序计算结果对比,取玻璃面板厚度11mm时,15组编号NO.6~20及编号NO.21~26相应表五NO.1~6,厚度8mm。
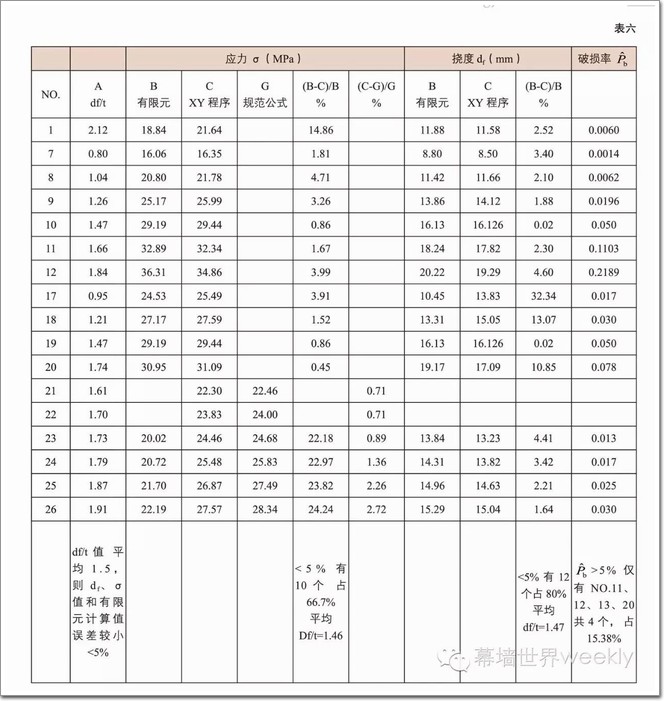

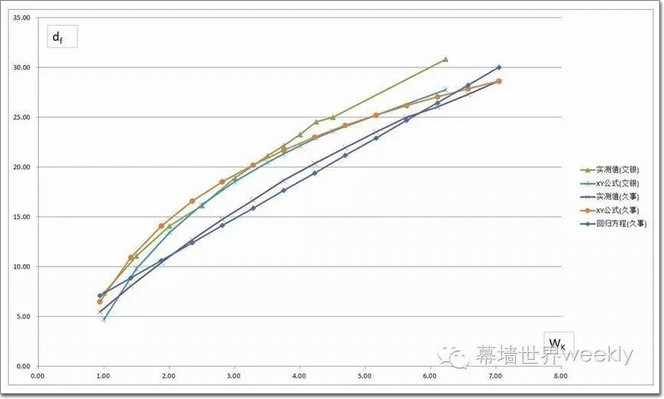


七、本文结论
1. 采用规范公式和几何非线性方法计算的玻璃面板σ、df值和实测值比较,误差较大;
2. 采用建立在玻璃试件微裂缝扩展试验基础上的经统计分析所得的经验回归公式计算的玻璃面板σ、df值和实测值比较,误差较小;
3. 中国幕墙玻璃面板为建立自主的适用计算方法,尚应进行大量试验实测工作。



关注微信平台
免费获取采购商机
![]()